Lcm Of 2 And 3
elan
Sep 12, 2025 · 6 min read
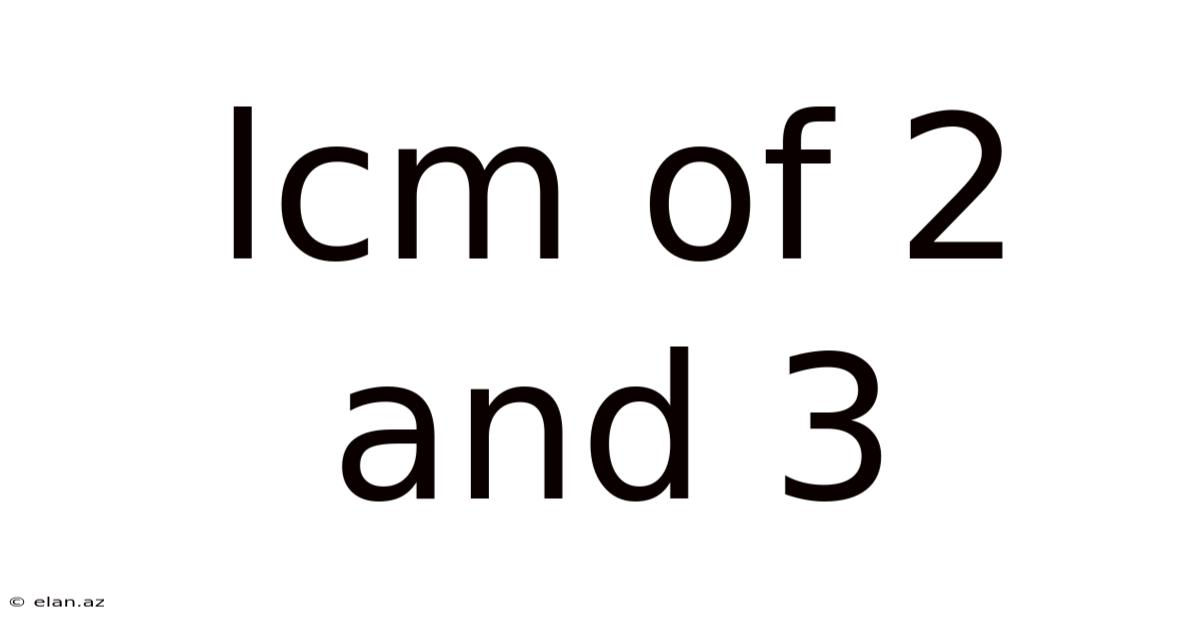
Table of Contents
Unveiling the Least Common Multiple (LCM) of 2 and 3: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, particularly when dealing with small numbers like 2 and 3. However, understanding the underlying concepts and methods involved opens a window into the fascinating world of number theory, with implications far beyond basic calculations. This comprehensive guide will not only reveal the LCM of 2 and 3 but also explore the broader context of LCMs, their applications, and different methods of calculation. We'll delve into the theoretical underpinnings, explain the practical implications, and answer frequently asked questions. By the end, you'll have a robust understanding of LCMs and their significance in mathematics.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific case of 2 and 3, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the integers can divide into without leaving a remainder.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 6 are 6, 12, 18, 24... The common multiples are 12, 24, 36... and the smallest of these common multiples is 12. Therefore, the LCM(4, 6) = 12.
Calculating the LCM of 2 and 3
Now, let's focus on our specific problem: finding the LCM of 2 and 3. Since 2 and 3 are relatively small numbers, we can use a simple method: listing the multiples.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
By comparing the lists, we can readily identify the common multiples: 6, 12, 18... The smallest common multiple is 6. Therefore, the LCM(2, 3) = 6.
Methods for Calculating LCMs: Beyond Listing Multiples
While listing multiples works well for small numbers, it becomes inefficient for larger numbers. Let's explore more efficient methods:
1. Prime Factorization Method
This method utilizes the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 3: 3 (3 is a prime number)
To find the LCM using prime factorization:
- List the prime factors of each number: 2 and 3.
- Identify the highest power of each prime factor present in the factorizations: In this case, the highest power of 2 is 2¹ and the highest power of 3 is 3¹.
- Multiply the highest powers together: 2¹ * 3¹ = 6. Therefore, the LCM(2, 3) = 6.
This method is more efficient for larger numbers because it avoids the tedious process of listing all multiples.
2. The Formula Using GCD (Greatest Common Divisor)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. For 2 and 3, the GCD is 1 (they share no common factors other than 1). The relationship between LCM and GCD is given by the formula:
LCM(a, b) * GCD(a, b) = a * b
Using this formula for 2 and 3:
LCM(2, 3) * GCD(2, 3) = 2 * 3 LCM(2, 3) * 1 = 6 LCM(2, 3) = 6
This method is particularly useful when dealing with larger numbers where finding the GCD is relatively easier than directly finding the LCM. Algorithms like the Euclidean algorithm efficiently calculate the GCD.
The Significance of LCMs: Real-World Applications
The concept of LCMs isn't just a theoretical exercise; it has practical applications in various fields:
-
Scheduling and Time Management: Imagine two buses departing from the same station, one every 2 hours and the other every 3 hours. The LCM(2, 3) = 6 determines when both buses will depart at the same time again – after 6 hours. This principle extends to scheduling meetings, production cycles, and other time-dependent events.
-
Fraction Operations: Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators. For example, to add 1/2 and 1/3, you need a common denominator, which is the LCM(2, 3) = 6. The calculation becomes (3/6) + (2/6) = 5/6.
-
Geometry and Measurement: LCMs are essential in solving problems related to lengths, areas, and volumes involving multiples of units. For instance, determining the shortest length that can be exactly measured using two different rulers with lengths of 2 and 3 units requires finding the LCM(2, 3) = 6 units.
-
Music Theory: The LCM plays a role in understanding musical intervals and harmony. The frequencies of musical notes are often related by ratios, and finding the LCM of these ratios helps in determining when notes will align harmoniously.
Expanding the Concept: LCMs of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method remains the most efficient:
- Find the prime factorization of each number.
- Identify the highest power of each prime factor present across all factorizations.
- Multiply these highest powers together to find the LCM.
For example, let's find the LCM(2, 3, 4):
- Prime factorizations: 2 = 2¹, 3 = 3¹, 4 = 2²
- Highest powers: 2² and 3¹
- LCM(2, 3, 4) = 2² * 3¹ = 12
Frequently Asked Questions (FAQ)
Q1: What if the GCD of two numbers is 0?
The GCD of two numbers is never 0 unless one or both of the numbers are 0. The GCD is always a positive integer.
Q2: Is the LCM always greater than the numbers involved?
No, the LCM is only greater than or equal to the largest of the numbers involved. If one number is a multiple of the other, the LCM is the larger number. For example, LCM(2, 4) = 4.
Q3: How do I find the LCM of very large numbers?
For very large numbers, the prime factorization method can become computationally expensive. More sophisticated algorithms, often implemented in computer programs, are used. These algorithms leverage the relationship between LCM and GCD and use efficient GCD calculation methods like the Euclidean algorithm.
Conclusion: Beyond the Basics of LCM(2,3)
While the LCM of 2 and 3, being 6, might appear trivial at first glance, exploring its calculation and underlying principles provides a firm foundation in number theory. We've seen that various methods exist for calculating LCMs, each with its strengths and weaknesses. Understanding these methods and their practical applications allows us to tackle more complex problems in mathematics and related fields. The journey from a simple arithmetic problem to a deeper understanding of number theory underscores the power of mathematical exploration and its surprising relevance in our everyday lives. The LCM, initially seemingly basic, reveals its depth and importance as we delve into its theoretical underpinnings and diverse real-world applications.
Latest Posts
Latest Posts
-
How Deep In The Earth
Sep 12, 2025
-
Is Displacement Scalar Or Vector
Sep 12, 2025
-
Words That Begin With Eg
Sep 12, 2025
-
Multiplication Times Table 1 20
Sep 12, 2025
-
Features Of Command Line Interface
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.