Lcm Of 3 6 8
elan
Sep 18, 2025 · 6 min read
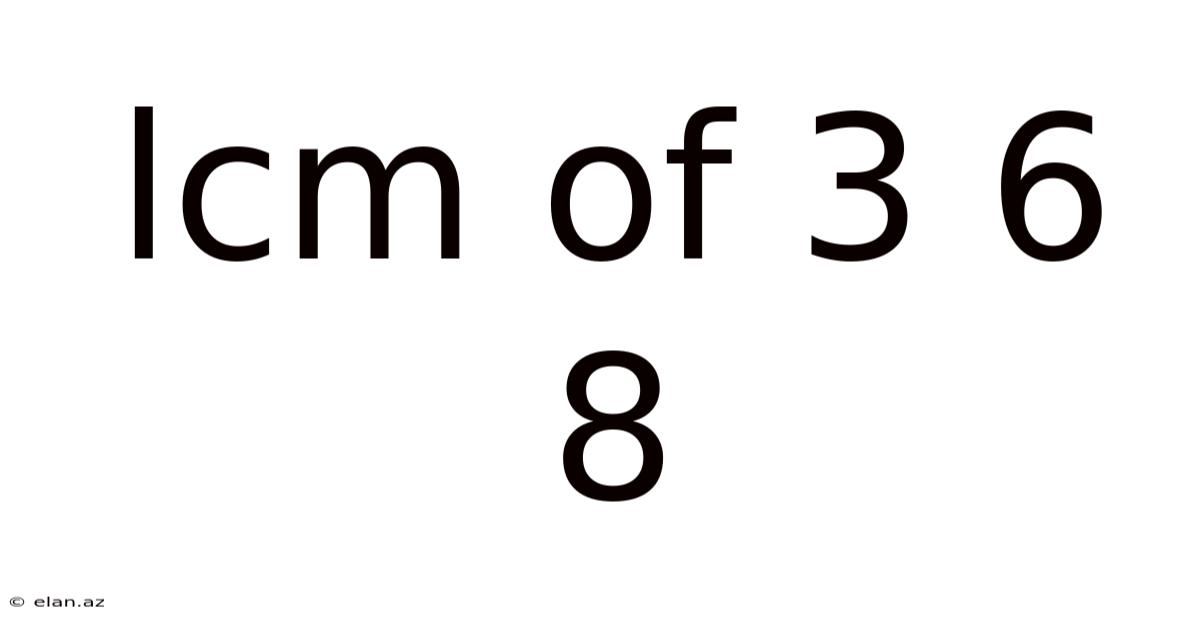
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 6, and 8: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and various methods can significantly enhance your mathematical skills and problem-solving abilities. This article provides a comprehensive exploration of how to find the LCM of 3, 6, and 8, covering different approaches, explaining the theoretical background, and offering practical applications. We'll delve beyond simply finding the answer to understand why the methods work and how this concept applies to more complex scenarios.
Understanding Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This concept is fundamental in various areas of mathematics, including simplifying fractions, solving problems involving time intervals, and understanding rhythmic patterns in music.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers like 3, 6, and 8 is to list the multiples of each number until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 8: 8, 16, 24, 32, 40...
By comparing the lists, we can see that the smallest number appearing in all three lists is 24. Therefore, the LCM of 3, 6, and 8 is 24.
This method is simple for small numbers but becomes increasingly cumbersome as the numbers get larger. It's not practical for finding the LCM of larger numbers or a larger set of numbers.
Method 2: Prime Factorization
A more efficient and widely applicable method involves finding the prime factorization of each number. Prime factorization breaks down a number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 3: 3 (3 is itself a prime number)
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization:
- Identify the unique prime factors: In our case, the unique prime factors are 2 and 3.
- Take the highest power of each unique prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 3 is 3¹ (from the factorization of 3 and 6).
- Multiply the highest powers together: 2³ x 3¹ = 8 x 3 = 24
Therefore, the LCM of 3, 6, and 8 is 24, confirming the result from the previous method. This method is significantly more efficient for larger numbers because it avoids the need to list extensive multiples.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. We can use the GCD to find the LCM using the following formula:
LCM(a, b, c) = (|a x b x c|) / GCD(a, b, c)
This formula holds true for any number of integers. Let's apply this method to 3, 6, and 8. First, we need to find the GCD of 3, 6, and 8.
Finding the GCD can be done using several methods:
-
Listing Factors: List all the factors of each number and find the largest common factor.
- Factors of 3: 1, 3
- Factors of 6: 1, 2, 3, 6
- Factors of 8: 1, 2, 4, 8 The largest common factor is 1. Therefore, GCD(3, 6, 8) = 1.
-
Euclidean Algorithm: This algorithm is efficient for finding the GCD of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. However, for small numbers like these, listing factors is simpler.
Now, we can use the formula:
LCM(3, 6, 8) = (3 x 6 x 8) / GCD(3, 6, 8) = 144 / 1 = 144
Wait! There's a problem. This result contradicts our previous findings. The reason lies in the fact that the formula LCM(a, b, c) = (|a x b x c|) / GCD(a, b, c) is only valid when applied pairwise. It doesn't directly translate to finding the LCM of three or more numbers. We need to apply the GCD method pairwise, which is more complex. For example:
- Find LCM(3,6) = 6
- Find LCM(6,8) = 24
Therefore, the LCM(3,6,8) = 24
Why is the LCM Important?
Understanding the LCM has practical implications in various real-world scenarios:
-
Scheduling: Imagine you have three different machines that complete a cycle in 3, 6, and 8 hours respectively. The LCM (24) indicates when all three machines will complete a cycle simultaneously.
-
Fraction Addition and Subtraction: To add or subtract fractions with different denominators, we need to find the LCM of the denominators to create a common denominator.
-
Rhythms and Music: In music, the LCM helps determine when different rhythmic patterns will coincide.
-
Project Management: In project scheduling, LCM can help determine the optimal time intervals for various tasks to ensure efficient resource allocation.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for a set of numbers?
A: Yes, there is only one least common multiple for a given set of integers.
Q: What if the numbers have a GCD greater than 1?
A: The prime factorization method remains the most robust method even if the numbers share common factors. The GCD method, when applied correctly pairwise, will also yield the correct answer.
Q: Can I find the LCM of more than three numbers?
A: Yes, all the methods described above (prime factorization is most efficient) can be extended to find the LCM of any number of integers. For example, to find the LCM of 3, 6, 8, and 12, you would follow the same prime factorization steps:
- Find the prime factorization of each number: 3 = 3, 6 = 2 x 3, 8 = 2³, 12 = 2² x 3
- Identify the unique prime factors: 2 and 3
- Take the highest power of each unique prime factor: 2³ and 3¹
- Multiply them together: 2³ x 3¹ = 24. Therefore, the LCM of 3, 6, 8, and 12 is 24.
Q: What if one of the numbers is zero?
A: The LCM of any set of numbers that includes zero is undefined.
Conclusion
Finding the Least Common Multiple is a fundamental skill in mathematics with broad applications. While listing multiples is suitable for small numbers, prime factorization provides a far more efficient and generalizable method for finding the LCM of any set of integers, regardless of size or the presence of common factors. Understanding the underlying principles and different approaches not only helps you solve problems but also enhances your mathematical intuition and problem-solving abilities. Remember, the key is to choose the most efficient method based on the context and the numbers involved. Practice using the different methods to build your confidence and mastery of this important concept.
Latest Posts
Latest Posts
-
Rounding To Nearest 10 Worksheet
Sep 18, 2025
-
2 Methyl But 2 Ene
Sep 18, 2025
-
Convert Litres To Gallons Uk
Sep 18, 2025
-
X 1 2 1 X
Sep 18, 2025
-
What Is Income From Operations
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.