Prime Factor Tree For 90
elan
Sep 11, 2025 · 6 min read
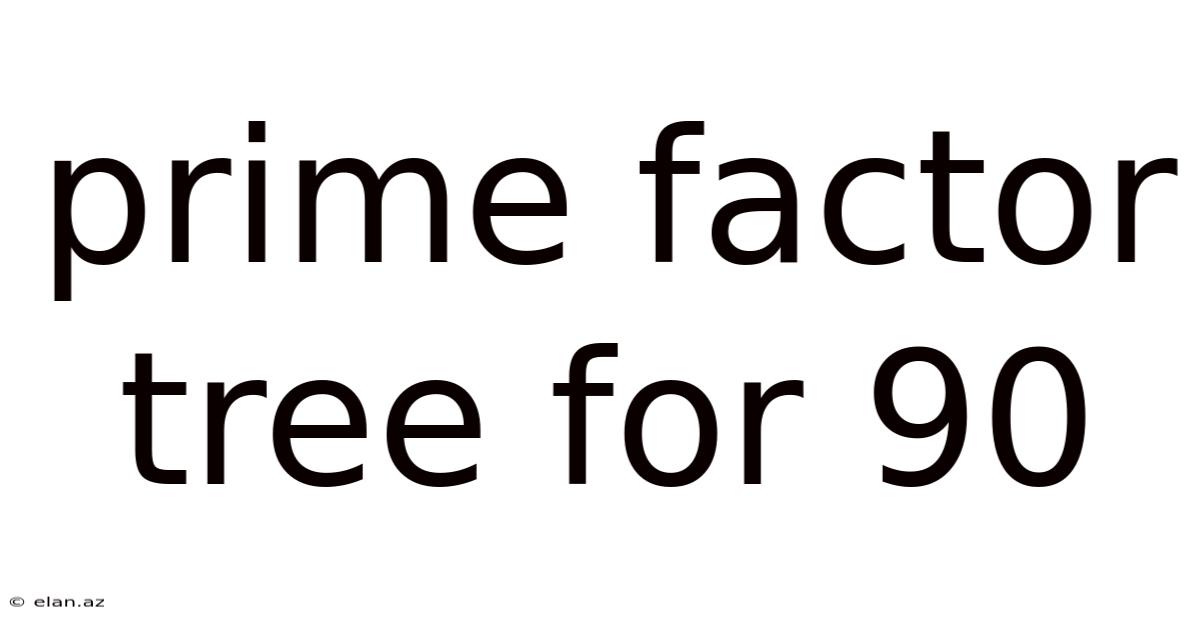
Table of Contents
Unveiling the Prime Factors of 90: A Comprehensive Guide to Prime Factorization using Factor Trees
Finding the prime factors of a number might seem like a dry mathematical exercise, but it's a fundamental concept with applications across various fields, from cryptography to computer science. This article will guide you through the process of finding the prime factors of 90 using a prime factor tree, explaining the concepts clearly and concisely. We'll delve into the definition of prime numbers, the importance of prime factorization, and explore the prime factor tree method in detail, using 90 as our example. We'll also address frequently asked questions to solidify your understanding of this vital mathematical tool.
Understanding Prime Numbers and Prime Factorization
Before diving into the factor tree, let's establish a firm understanding of the key terms. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
Prime factorization is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number; meaning there's only one way to express a number as a product of primes (ignoring the order). Prime factorization is crucial because it simplifies many mathematical operations and underlies various algorithms in computer science and cryptography.
Constructing the Prime Factor Tree for 90
Now, let's construct the prime factor tree for 90. A prime factor tree is a visual representation of the factorization process. We start by finding any two factors of 90 and branching them off from the original number. We continue this process for each composite factor until we're left with only prime numbers at the end of each branch.
Here's how we can do it for 90:
-
Start with 90: We begin by writing 90 at the top of our tree.
-
Find two factors: We can choose any two factors of 90. Let's choose 9 and 10. These become the first branches of our tree.
-
Continue branching: 9 is not a prime number; its factors are 3 and 3 (both prime). 10 is also not prime; its factors are 2 and 5 (both prime). We branch these off from 9 and 10 respectively.
-
Identify the prime factors: We have reached the end of our branches, and all the numbers at the bottom are prime: 2, 3, 3, and 5.
Visually, the prime factor tree for 90 would look like this:
90
/ \
9 10
/ \ / \
3 3 2 5
Therefore, the prime factorization of 90 is 2 x 3 x 3 x 5, or 2 x 3² x 5.
Alternative Prime Factor Trees for 90
It's important to note that you can arrive at the same prime factorization even if you choose different initial factors. Let's demonstrate this with an alternative approach:
-
Start with 90: Again, we begin with 90.
-
Find different factors: This time, let's use 2 and 45 as our initial factors.
-
Continue branching: 2 is already a prime number. 45 is not; its factors are 9 and 5. 9 further factors into 3 and 3 (both prime), and 5 is already prime.
-
Identify prime factors: The prime factors at the bottom of the tree are again 2, 3, 3, and 5.
The alternative tree would look like this:
90
/ \
2 45
/ \
9 5
/ \
3 3
As you can see, regardless of the initial factors chosen, the final prime factorization remains the same: 2 x 3² x 5. This highlights the uniqueness of prime factorization.
The Importance of Prime Factorization
The process of finding prime factors might seem tedious, but it's a cornerstone of number theory and has significant applications in various fields. Some key applications include:
-
Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization provides a straightforward method to find the GCD and LCM of two or more numbers. This is extremely useful in simplifying fractions and solving problems in algebra.
-
Cryptography: Many encryption algorithms rely on the difficulty of factoring large numbers into their prime components. The security of these systems depends on this computational challenge.
-
Simplifying Fractions: Prime factorization helps in simplifying fractions to their lowest terms by identifying common factors in the numerator and denominator.
-
Solving Diophantine Equations: Certain types of equations involving integers can be solved efficiently using prime factorization techniques.
-
Computer Science: Algorithms in computer science often utilize prime numbers and prime factorization for tasks such as hashing, data compression, and random number generation.
Beyond the Basics: Exploring Different Methods
While the prime factor tree is a visually intuitive method, other techniques can also be used to find prime factors. These include:
-
Division by Primes: Systematically divide the number by the smallest prime numbers (2, 3, 5, 7, etc.) until you obtain a quotient of 1. The prime numbers used in the divisions are the prime factors.
-
Using Algorithms: More sophisticated algorithms exist for factoring larger numbers, especially those used in cryptography. These algorithms are beyond the scope of this introductory guide.
Frequently Asked Questions (FAQ)
Q1: What if I choose different factors at the beginning of the prime factor tree? Will I get a different answer?
A1: No, you will not get a different answer. The prime factorization of a number is unique. While different paths may be taken in the tree, the prime numbers at the end will always be the same.
Q2: Is there a limit to how large a number can be prime factorized?
A2: Theoretically, there is no limit. However, practically, factoring extremely large numbers becomes computationally intensive and time-consuming, especially for numbers used in cryptography.
Q3: What is the significance of the exponent in the prime factorization (e.g., 3² in the factorization of 90)?
A3: The exponent indicates how many times that prime factor appears in the factorization. In the case of 90 (2 x 3² x 5), the prime factor 3 appears twice.
Q4: Why is prime factorization important in simplifying fractions?
A4: By finding the prime factors of the numerator and denominator, we can easily identify common factors that can be cancelled out, resulting in a simplified fraction in its lowest terms.
Q5: Can I use a calculator to help me find prime factors?
A5: While calculators can help with basic calculations, they don’t directly provide prime factorization. However, some advanced calculators might have built-in functions to assist with this process. Understanding the underlying method is crucial, even if you utilize computational aids.
Conclusion
Prime factorization, though seemingly a simple concept, is a powerful tool with wide-ranging applications. The prime factor tree method offers a clear and visual approach to understanding this fundamental process. By understanding prime numbers and their unique role in factorization, you unlock a key to many advanced mathematical concepts and appreciate the elegance and power of prime numbers in various fields. Remember, the key is to practice! The more you work with prime factorization, the more comfortable and confident you will become in solving these types of problems. So grab a pencil and paper and try factoring some more numbers! You’ll soon discover the fascinating world of prime numbers and their many applications.
Latest Posts
Latest Posts
-
Prime Factor Decomposition Of 252
Sep 11, 2025
-
600 Sq Ft In M
Sep 11, 2025
-
Lcm Of 42 And 385
Sep 11, 2025
-
Formula Of Perimeter Of Sector
Sep 11, 2025
-
Barium Chloride And Sodium Sulfate
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.