What Is 10 Of 1200
elan
Sep 12, 2025 · 5 min read
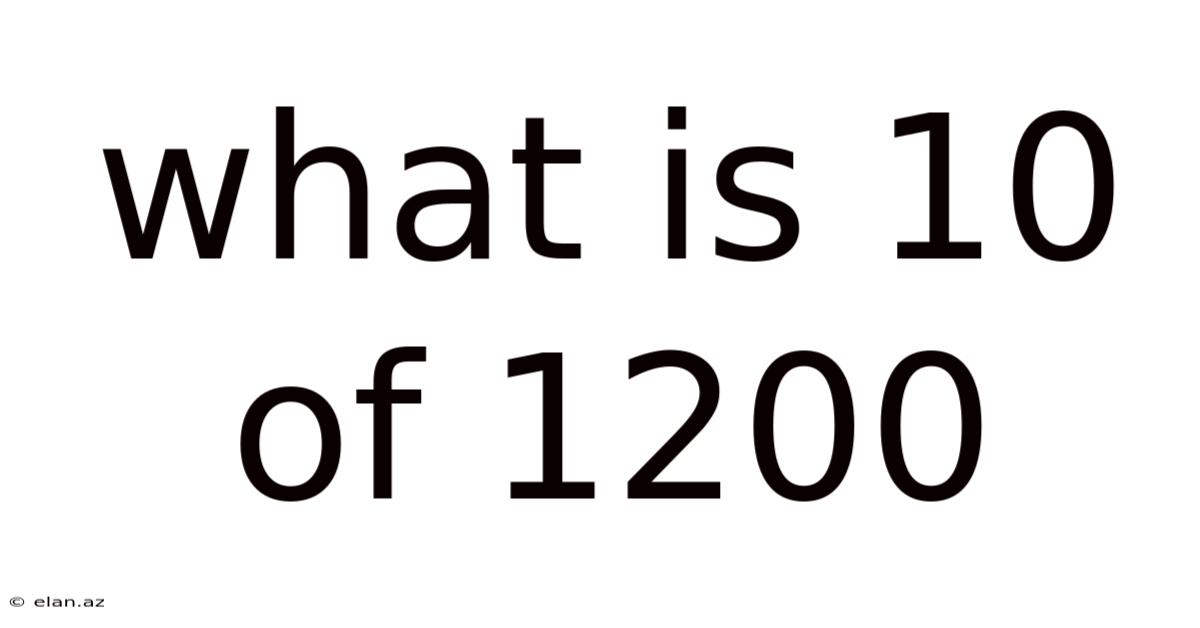
Table of Contents
What is 10% of 1200? A Comprehensive Guide to Percentages and Their Applications
Finding 10% of 1200 is a simple percentage calculation, but understanding the underlying principles can unlock a world of practical applications in various fields, from everyday budgeting to complex financial analysis. This article provides a detailed explanation of how to calculate 10% of 1200, explores the concept of percentages, and delves into various real-world examples. We will also address common misconceptions and frequently asked questions.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 10% means 10 out of every 100, or 10/100, which simplifies to 1/10 or 0.1 as a decimal. This understanding forms the basis for all percentage calculations.
Calculating 10% of 1200: The Simple Method
The simplest way to calculate 10% of 1200 is to multiply 1200 by 0.1 (the decimal equivalent of 10%).
- 1200 x 0.1 = 120
Therefore, 10% of 1200 is 120.
Calculating 10% of 1200: The Mental Math Approach
For a quicker calculation, especially with multiples of 10, you can use mental math. Since 10% is one-tenth, finding 10% of a number is the same as dividing that number by 10.
- 1200 / 10 = 120
This method is efficient and helpful for quick estimations in various situations.
Beyond the Basics: Understanding Percentage Applications
The ability to calculate percentages extends far beyond simple arithmetic. Understanding percentages is crucial in many areas of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding the interest rate on a loan or the annual percentage yield (APY) on a savings account is critical for making informed financial decisions.
-
Retail: Discounts are commonly expressed as percentages. If a store offers a 20% discount on an item priced at $100, the discount amount is 20% of $100, which is $20. The final price after the discount would be $80.
-
Science and Statistics: Percentages are used extensively to represent data and probabilities. For example, researchers might report that 75% of participants in a study showed a certain response, or a weather forecast might predict a 60% chance of rain.
-
Everyday Life: Tips in restaurants, calculating sales tax, or figuring out the percentage of ingredients in a recipe all involve percentage calculations.
Advanced Percentage Calculations: Finding Other Percentages of 1200
While we've focused on 10%, let's explore how to calculate other percentages of 1200 to broaden your understanding. The general formula is:
(Percentage/100) x Number
- Finding 25% of 1200: (25/100) x 1200 = 0.25 x 1200 = 300
- Finding 50% of 1200: (50/100) x 1200 = 0.5 x 1200 = 600 (This is simply half of 1200)
- Finding 75% of 1200: (75/100) x 1200 = 0.75 x 1200 = 900
- Finding 15% of 1200: (15/100) x 1200 = 0.15 x 1200 = 180
These examples demonstrate the versatility of the percentage calculation and its application to different numerical scenarios.
Working Backwards: Finding the Original Number
Sometimes, you might know the percentage and the resulting value, and need to find the original number. For example, if 10% of a number is 120, what is the original number? To solve this:
- Divide the known value by the percentage (expressed as a decimal): 120 / 0.1 = 1200
This demonstrates the reverse process of percentage calculation, which is equally important in various problem-solving scenarios.
Practical Examples of Percentage Applications
Let's delve into some real-world examples to solidify our understanding:
Example 1: Restaurant Tip
You had a dinner bill of $1200 and want to leave a 15% tip. The calculation is:
(15/100) x 1200 = $180 tip
Example 2: Sales Tax
You purchase an item for $1200, and the sales tax is 6%. The sales tax amount is:
(6/100) x 1200 = $72
The total cost, including tax, is $1200 + $72 = $1272
Example 3: Investment Returns
You invested $1200 and earned a 10% return on your investment. Your profit is:
(10/100) x 1200 = $120
Your total investment value is now $1200 + $120 = $1320
Common Misconceptions about Percentages
-
Adding Percentages Directly: A common mistake is to add percentages directly without considering the base value. For example, if you have a 10% increase followed by a 10% decrease, the final value is not the same as the original value.
-
Confusing Percentage Change with Absolute Change: Percentage change expresses the relative change compared to the original value, while absolute change is the actual numerical difference. Understanding the distinction is crucial for accurate interpretation of data.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new and original value, divide this difference by the original value, and multiply by 100. A percentage decrease is calculated similarly.
-
Q: What is the difference between a percentage and a proportion?
A: While closely related, a proportion is a ratio of two numbers, while a percentage is a specific type of proportion expressed as a fraction of 100.
-
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100%, indicating an increase beyond the original value. For example, a 150% increase means the final value is 2.5 times the original value.
-
Q: Are there any online calculators for percentage calculations?
A: Yes, many websites offer online calculators that can perform various percentage calculations.
Conclusion
Calculating 10% of 1200, as demonstrated, is a straightforward process. However, understanding the broader concept of percentages and their applications is crucial for various aspects of life. From managing personal finances to interpreting statistical data, mastering percentage calculations empowers you to make informed decisions and solve problems effectively. This comprehensive guide has provided not only the solution to the initial question but also a deeper understanding of percentages and their wide-ranging applications. Remember to practice regularly to build your proficiency and confidence in tackling various percentage-related problems.
Latest Posts
Latest Posts
-
Names Of Parts Of Circles
Sep 12, 2025
-
Characteristic Gas Constant Of Air
Sep 12, 2025
-
What Is The Resonance Frequency
Sep 12, 2025
-
Lcm Of 105 And 770
Sep 12, 2025
-
6 Letter Words Ending E
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.