What Is 10 Of 30000
elan
Sep 20, 2025 · 5 min read
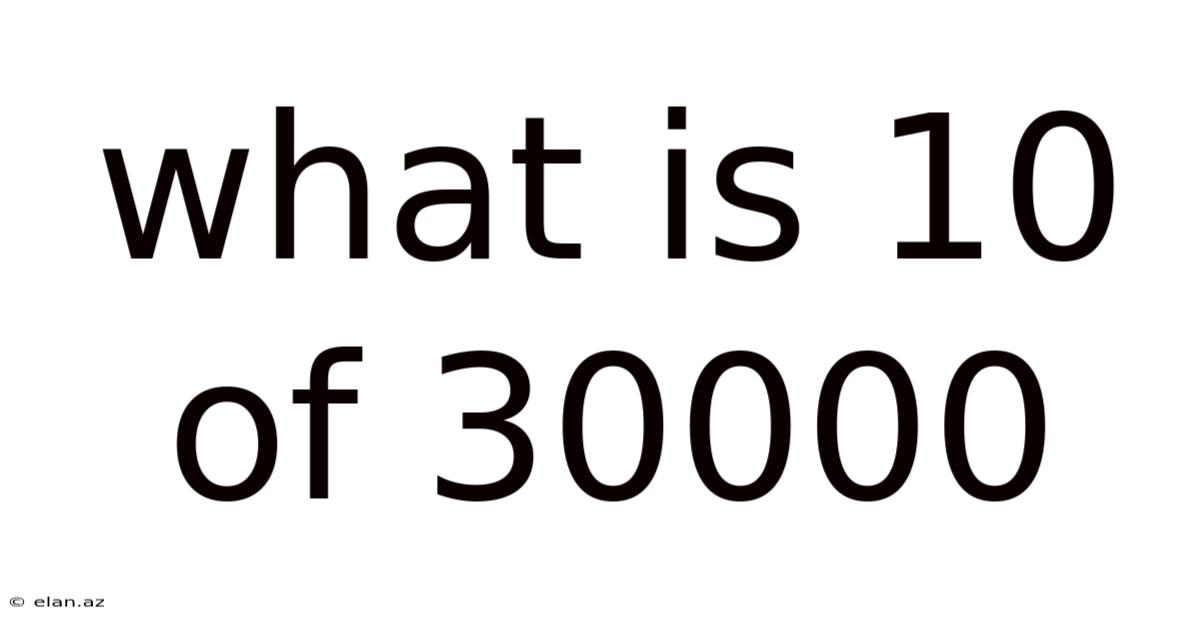
Table of Contents
What is 10% of 30,000? A Deep Dive into Percentages and Their Applications
Finding 10% of 30,000 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages opens the door to a world of practical applications in various fields, from finance and budgeting to data analysis and scientific research. This article will not only answer the question directly but also explore the concept of percentages in detail, offering various methods for calculating them and highlighting their real-world significance.
Introduction: Understanding Percentages
A percentage is simply a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin per centum, meaning "out of a hundred". Percentages are a convenient way to represent proportions and make comparisons between different quantities. They are ubiquitous in everyday life, appearing in discounts, interest rates, tax calculations, statistical data, and much more. Understanding percentages is a fundamental skill applicable across diverse fields.
Method 1: The Direct Calculation Method
The most straightforward way to find 10% of 30,000 is to directly apply the definition of percentage. 10% means 10 out of 100, which can be expressed as the fraction 10/100 or the decimal 0.10. To find 10% of 30,000, we simply multiply 30,000 by 0.10:
30,000 x 0.10 = 3,000
Therefore, 10% of 30,000 is 3,000.
Method 2: Using Fractions
We can also approach this problem using fractions. 10% is equivalent to the fraction 1/10. To find 1/10 of 30,000, we divide 30,000 by 10:
30,000 / 10 = 3,000
This method confirms that 10% of 30,000 is indeed 3,000. This method is particularly helpful when dealing with percentages that are easily expressed as simple fractions, such as 25% (1/4), 50% (1/2), or 75% (3/4).
Method 3: Using Proportions
Another approach involves setting up a proportion. We can express the problem as:
10/100 = x/30,000
Where 'x' represents the unknown value (10% of 30,000). To solve for 'x', we cross-multiply:
10 * 30,000 = 100 * x
300,000 = 100x
x = 300,000 / 100
x = 3,000
Again, this method confirms that 10% of 30,000 is 3,000. This method is useful for solving more complex percentage problems where the percentage or the base value is unknown.
Beyond the Basics: Applications of Percentages
The seemingly simple calculation of finding 10% of 30,000 has far-reaching implications in numerous practical situations. Let's explore some key applications:
-
Financial Calculations: Percentages are fundamental to various financial computations. Calculating interest on loans or savings accounts, determining discounts on purchases, understanding tax rates, and analyzing investment returns all rely heavily on percentage calculations. For instance, a 10% discount on a $30,000 car would represent a savings of $3,000.
-
Data Analysis and Statistics: Percentages are essential for interpreting and presenting statistical data. For example, understanding the percentage change in sales figures, analyzing survey results, or representing demographic distributions often involves percentage calculations. If a survey of 30,000 people shows that 10% support a particular policy, this indicates 3,000 supporters.
-
Scientific Research: Percentages are widely used in scientific research to express experimental results, quantify variations, and make comparisons between different groups or conditions. For instance, the percentage of successful trials in a clinical experiment is crucial for evaluating the effectiveness of a treatment.
-
Everyday Life: From calculating tips in restaurants (often 10%, 15%, or 20%) to understanding the nutritional content of food (e.g., percentage of daily value of vitamins), percentages are integral to our daily interactions with numbers.
Understanding Percentage Change
It's also important to understand the concept of percentage change, which measures the relative change in a value over time or between two different points. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100%
For instance, if the value increases from 30,000 to 33,000, the percentage change would be:
[(33,000 - 30,000) / 30,000] * 100% = 10%
This indicates a 10% increase. Conversely, if the value decreased from 30,000 to 27,000, the percentage change would be -10%, representing a 10% decrease.
Solving More Complex Percentage Problems
While finding 10% of 30,000 is relatively straightforward, let's consider more intricate scenarios:
-
Finding x% of y: The general formula for finding x% of y is: (x/100) * y. This allows you to calculate any percentage of any value.
-
Finding the original value: If you know the percentage and the resulting value, you can calculate the original value. For instance, if 10% of a value is 3,000, the original value can be calculated as: 3,000 / 0.10 = 30,000.
-
Calculating percentage increase or decrease: As mentioned earlier, the percentage change formula helps determine the relative change between two values.
-
Compound interest: Calculating compound interest involves repeated percentage calculations over time, reflecting the effect of earning interest on both the principal and accumulated interest.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
- A: The easiest method often depends on the specific percentage and values involved. For simple percentages like 10%, direct multiplication by the decimal equivalent (0.10) is often quickest. For other percentages, using a calculator or spreadsheet software can be efficient.
-
Q: How can I improve my percentage calculation skills?
- A: Practice is key! Work through various percentage problems, starting with simple ones and gradually increasing the complexity. Understanding the underlying principles and different calculation methods is also essential.
-
Q: Are there any online tools or calculators for calculating percentages?
- A: Yes, numerous online percentage calculators are readily available. These tools can be helpful for quick calculations or verifying your own work. However, understanding the underlying principles remains crucial for broader application.
-
Q: What are some common mistakes people make when calculating percentages?
- A: Common errors include incorrect decimal placement, confusing percentage increase and decrease calculations, and not understanding the context of the problem. Careful attention to detail and a methodical approach can minimize these errors.
Conclusion: The Power of Percentages
The seemingly simple calculation of 10% of 30,000 serves as a gateway to understanding the broader significance of percentages. From basic arithmetic to complex financial modeling and scientific analysis, percentages are an indispensable tool for representing proportions, making comparisons, and interpreting data. Mastering percentage calculations is not just about solving mathematical problems; it's about gaining a crucial skill applicable across diverse fields and enhancing your ability to understand and interpret the quantitative world around you. By grasping the fundamental principles and practicing various calculation methods, you can unlock the power of percentages and apply them effectively in your academic, professional, and personal life.
Latest Posts
Latest Posts
-
Footprints In The Sand Pdf
Sep 20, 2025
-
Shortcut Of Filter In Excel
Sep 20, 2025
-
How To Calculate Photosynthesis Rate
Sep 20, 2025
-
What Is An Isotonic Solution
Sep 20, 2025
-
Lcm Of 50 And 525
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 30000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.