X 2 X 3 6
elan
Sep 24, 2025 · 5 min read
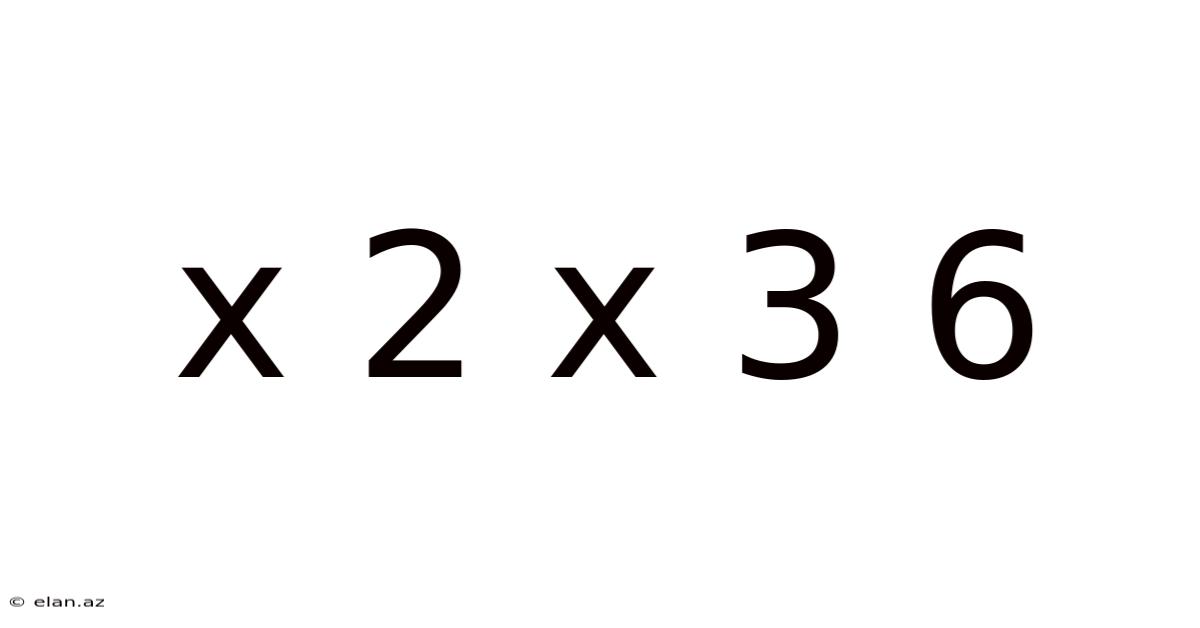
Table of Contents
Decoding the Simplicity of 2 x 3 = 6: A Deep Dive into Multiplication and its Applications
The seemingly simple equation, 2 x 3 = 6, forms the bedrock of mathematics. While elementary school students readily grasp its solution, its implications extend far beyond basic arithmetic. This article explores the multifaceted nature of this equation, delving into the fundamental concepts of multiplication, its practical applications, and its significance in higher-level mathematics and everyday life. We'll uncover the underlying principles, examine different approaches to understanding multiplication, and explore its relevance across various disciplines.
Understanding Multiplication: Beyond Simple Repetition
At its core, multiplication is repeated addition. 2 x 3 can be visualized as adding two, three times: 2 + 2 + 2 = 6. This conceptualization is crucial for younger learners to grasp the underlying meaning of multiplication before progressing to more complex calculations. However, understanding multiplication extends beyond mere repetition. It represents a fundamental relationship between quantities, a scaling factor, or a way to efficiently calculate the total number of items in a group.
Visualizing Multiplication: Imagine two groups of three apples. To find the total number of apples, we can either count each apple individually or use multiplication. The equation 2 x 3 = 6 directly provides the answer, representing two groups multiplied by three items per group. This visualization helps solidify the concept, especially for visual learners.
The Commutative Property: A key property of multiplication is its commutative nature. This means that the order of the numbers doesn't affect the outcome. 2 x 3 is the same as 3 x 2, both equaling 6. This seemingly small detail has significant implications, allowing for flexibility in problem-solving.
Different Approaches to Multiplication: Catering to Diverse Learning Styles
Teaching multiplication effectively involves catering to different learning styles. While repeated addition works well for some, others benefit from different approaches:
-
Arrays: Visualizing numbers in a grid or array can be helpful. A 2 x 3 array shows two rows of three items each, immediately revealing a total of six items. This method strengthens the connection between multiplication and geometry.
-
Skip Counting: Skip counting, where you count by a specific number (in this case, 2), three times (2, 4, 6) is an effective way to understand multiplication, especially for kinesthetic learners who benefit from active participation.
-
Number Lines: Using a number line, you can visualize jumps of 2, three times, landing on 6. This approach makes the process more tangible and less abstract.
-
Real-World Examples: Connecting multiplication to real-world scenarios makes it more relatable. Examples like calculating the total cost of three items at $2 each or determining the number of legs on two tables with three legs each bring the concept to life.
The Significance of 2 x 3 = 6 in Higher Mathematics
While seemingly basic, the equation 2 x 3 = 6 lays the foundation for more advanced mathematical concepts:
-
Algebra: This simple equation is a building block for algebraic expressions and equations. Understanding multiplication allows for manipulating variables and solving complex problems. It's a cornerstone for understanding concepts like distributive property (a(b+c) = ab + ac).
-
Calculus: Calculus relies heavily on the concept of limits and derivatives, both involving multiplicative relationships between infinitesimally small changes. The understanding of basic multiplication is essential for grasping these more complex concepts.
-
Linear Algebra: Matrices and vectors, fundamental elements of linear algebra, involve multiplication operations to perform transformations and solve systems of equations. The principles established in simple multiplication are directly applied here.
-
Number Theory: Prime factorization, a crucial concept in number theory, relies on repeatedly multiplying prime numbers to arrive at composite numbers. The relationship expressed in 2 x 3 = 6 illustrates the essence of prime factorization.
Applications of Multiplication in Everyday Life
Multiplication isn't confined to the classroom; it's integral to our daily lives:
-
Shopping: Calculating the total cost of multiple items, determining discounts, and calculating taxes all involve multiplication.
-
Cooking: Following recipes often requires multiplying ingredient quantities to adjust for different serving sizes.
-
Travel: Calculating distances, fuel consumption, and travel time often involves multiplication.
-
Finance: Calculating interest, managing budgets, and investing all require a solid understanding of multiplication.
-
Construction: Calculating the amount of material needed for a project, estimating costs, and measuring dimensions frequently require multiplication.
-
Technology: From processing images to running complex algorithms, many technological applications rely heavily on multiplication.
Addressing Common Misconceptions and FAQs
Many learners, especially young children, encounter certain misconceptions regarding multiplication. Addressing these early on prevents future difficulties:
Q: What if I multiply in a different order? Will I get a different answer?
A: No, multiplication is commutative, meaning the order doesn't affect the result. 2 x 3 is the same as 3 x 2.
Q: Why is multiplication important? Can't I just add everything up?
A: While adding works for small numbers, multiplication is far more efficient for larger numbers. Imagine adding 2 fifty times versus multiplying 2 x 50. Multiplication saves time and reduces the risk of errors.
Q: What if I forget the multiplication table?
A: Don't worry! It's okay to use other methods like repeated addition, arrays, or skip counting to find the answer. The multiplication table is a tool, but understanding the underlying concept is more important.
Q: How can I improve my multiplication skills?
A: Practice is key! Regularly solving multiplication problems, using different methods, and applying multiplication to real-world scenarios will significantly enhance your skills. Games and interactive learning resources can also make the learning process more engaging and effective.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple equation, 2 x 3 = 6, is far more significant than it initially appears. It embodies fundamental mathematical concepts that extend into advanced mathematical fields and numerous applications in everyday life. Understanding multiplication, not just as a rote procedure but as a fundamental relationship between quantities, provides a solid foundation for future learning and problem-solving abilities. The ability to grasp this simple equation opens doors to a world of mathematical possibilities, shaping our understanding of numbers and their relationships, both in the abstract and in the practical realities of our daily lives. It highlights the power of seemingly simple concepts in building a deep and comprehensive understanding of the world around us. Through varied approaches to learning and consistent practice, mastering this fundamental concept empowers individuals to approach more complex mathematical challenges with confidence and competence.
Latest Posts
Latest Posts
-
Melting Point Of Tungsten Metal
Sep 24, 2025
-
14 20 As A Percent
Sep 24, 2025
-
Free Crossword Clue 3 Letters
Sep 24, 2025
-
2 11 As A Recurring Decimal
Sep 24, 2025
-
10 12 As A Percent
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.