Hcf Of 8 And 18
elan
Sep 14, 2025 · 6 min read
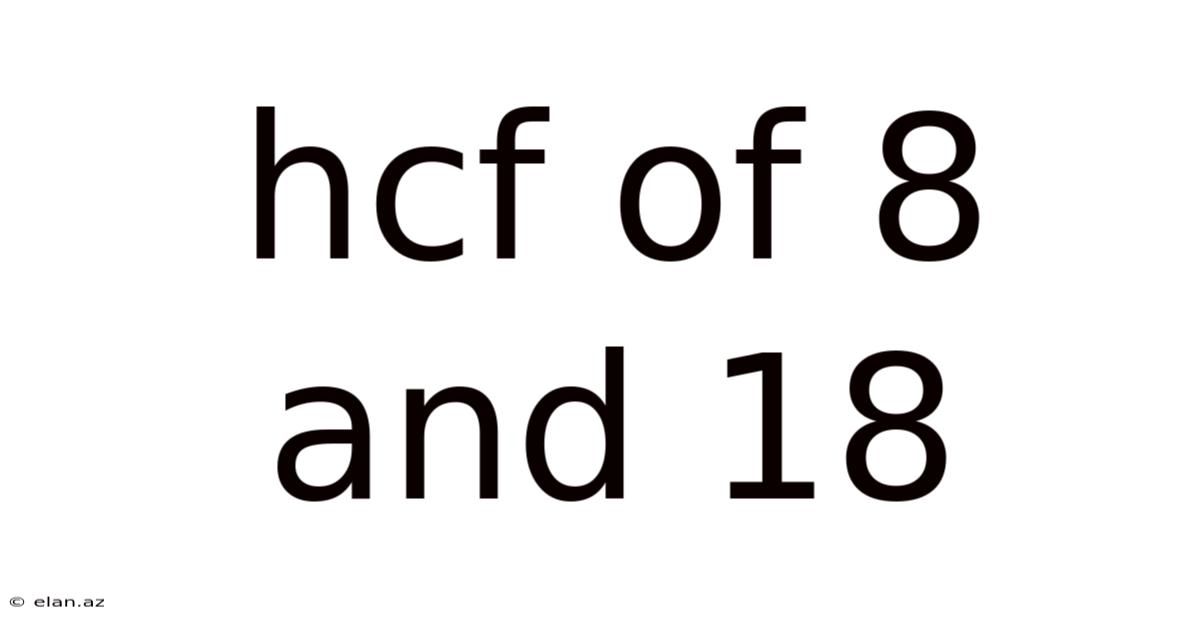
Table of Contents
Finding the Highest Common Factor (HCF) of 8 and 18: A Comprehensive Guide
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve deep into determining the HCF of 8 and 18, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll cover prime factorization, the Euclidean algorithm, and even touch upon the application of HCF in real-world scenarios. By the end, you'll not only know the HCF of 8 and 18 but also possess a strong grasp of this crucial mathematical concept.
Understanding Highest Common Factor (HCF)
The HCF of two or more numbers is the largest number that divides each of them without leaving a remainder. It's the biggest factor common to all the numbers in question. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6, therefore, the HCF of 12 and 18 is 6.
Method 1: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Let's find the HCF of 8 and 18 using this method:
-
Find the prime factorization of 8: 8 = 2 x 2 x 2 = 2³
-
Find the prime factorization of 18: 18 = 2 x 3 x 3 = 2 x 3²
-
Identify common prime factors: Both 8 and 18 share one common prime factor: 2.
-
Determine the HCF: The HCF is the product of the common prime factors raised to the lowest power. In this case, the lowest power of the common prime factor 2 is 2¹. Therefore, the HCF of 8 and 18 is 2.
Method 2: Listing Factors
This method involves listing all the factors of each number and identifying the largest common factor.
-
List the factors of 8: 1, 2, 4, 8
-
List the factors of 18: 1, 2, 3, 6, 9, 18
-
Identify common factors: The common factors of 8 and 18 are 1 and 2.
-
Determine the HCF: The largest common factor is 2. Therefore, the HCF of 8 and 18 is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF of two numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to find the HCF of 8 and 18:
-
Start with the larger number (18) and the smaller number (8).
-
Divide the larger number (18) by the smaller number (8): 18 ÷ 8 = 2 with a remainder of 2.
-
Replace the larger number with the remainder (2). Now we have the numbers 8 and 2.
-
Repeat the process: 8 ÷ 2 = 4 with a remainder of 0.
-
Since the remainder is 0, the HCF is the last non-zero remainder, which is 2. Therefore, the HCF of 8 and 18 is 2.
Visualizing the HCF: Venn Diagrams
A Venn diagram can be a helpful visual tool to understand the concept of HCF. We represent the factors of each number in separate circles, and the overlapping area represents the common factors.
For 8 and 18:
- Circle 1 (Factors of 8): 1, 2, 4, 8
- Circle 2 (Factors of 18): 1, 2, 3, 6, 9, 18
The overlapping area (common factors) contains 1 and 2. The largest number in the overlapping area is 2, hence the HCF is 2.
Why is finding the HCF important?
Finding the HCF is not just an abstract mathematical exercise. It has practical applications in various fields:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and denominator by their HCF.
-
Solving Word Problems: Many word problems involving division and sharing require finding the HCF to obtain the largest possible equal groups or shares. For instance, if you have 8 apples and 18 oranges, and you want to divide them into the largest possible equal groups with the same number of apples and oranges in each group, the HCF (2) tells you that you can create 2 equal groups.
-
Geometry: HCF is used in finding the dimensions of the largest square tile that can be used to cover a rectangular floor without any gaps or overlaps.
-
Music: HCF is used in music theory to find the greatest common divisor of two note frequencies, which helps determine the musical intervals.
-
Computer Science: The Euclidean algorithm, used for finding HCF, is fundamental in various computer algorithms and cryptographic applications.
Beyond 8 and 18: Extending the Concepts
The methods described above – prime factorization, listing factors, and the Euclidean algorithm – can be applied to find the HCF of any two (or more) numbers. For larger numbers, the Euclidean algorithm is generally the most efficient method.
For example, let's find the HCF of 24 and 36 using the Euclidean algorithm:
- 36 ÷ 24 = 1 remainder 12
- 24 ÷ 12 = 2 remainder 0
The HCF of 24 and 36 is 12.
Frequently Asked Questions (FAQ)
-
What if the HCF of two numbers is 1? If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Can the HCF of two numbers be larger than the smaller number? No, the HCF can never be larger than the smaller of the two numbers.
-
How do I find the HCF of more than two numbers? You can extend the methods described above, particularly the Euclidean algorithm, to find the HCF of multiple numbers. You would find the HCF of the first two numbers, then find the HCF of that result and the third number, and so on.
-
Are there any online calculators to find the HCF? Yes, numerous online calculators are available to find the HCF of any set of numbers quickly and easily. However, understanding the underlying concepts and methods is crucial for developing a strong mathematical foundation.
Conclusion
Finding the highest common factor is a critical skill in mathematics with practical applications in various fields. We've explored three different methods – prime factorization, listing factors, and the Euclidean algorithm – to determine the HCF of 8 and 18, which is 2. Understanding these methods and their underlying principles will not only help you solve problems involving HCF but also enhance your overall mathematical understanding. Remember that the Euclidean algorithm is often the most efficient method for larger numbers. Mastering these techniques will equip you with valuable problem-solving skills applicable well beyond the classroom. Practice makes perfect; so keep exploring and experimenting with different numbers to solidify your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Easy To Understand 8 Letters
Sep 14, 2025
-
2 10 As A Percent
Sep 14, 2025
-
How Long Is 3 Km
Sep 14, 2025
-
Cu M To Sq Ft
Sep 14, 2025
-
Graph Of Y 2x 1
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 8 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.